
Note: Following a remark by Sextus Empiricus I add that when writing about "frequentists" and "Bayesians" I don't intend to imply that anybody has to be either a frequentist or a Bayesian as a person. However a Bayesian still can think of a real process as a sampling process for choosing and processing their epistemic probabilities, in which case something can occur in the Bayesian computations that looks and acts like a sampling distribution. They don't "bypass" it, it is a concept that isn't meaningful for them. As there is no such thing in epistemic probability as an underlying real process defining probabilities, they don't have a sampling distribution in this sense. The concept of a "sampling distribution" is understood by frequentists as referring to a distribution of a statistic given that data are distributed according to the underlying real process. A frequentist probability would be defined by a data generating process in reality, whereas an epistemic probability refers to a state of knowledge of an individual (or science as a whole) about something rather than the real process that generates this "something". "Bayesian" on the other hand is often meant refer to a particular interpretation of the meaning of probability, usually understood as "epistemic" probabilities, although this is not the only possible meaning "Bayesian" can have. These rely crucially on the sampling distribution.


However more people use "frequentist" as referring to what is known as standard frequentist approaches to inference, estimation, tests and confidence regions. In this sense one can be a frequentist without ever computing confidence intervals, and as a frequentist one can do Bayesian statistics (particularly if the prior has a frequentist interpretation). "Frequentism" can be understood as adhering to a specific interpretation of the meaning of probability, which doesn't necessarily imply that any specific methodology needs to be applied. We need to be precise about the terms "frequentist" and "Bayesian", because they are ambiguous. If the posterior distribution does not follow any known distribution, we just use our simulated distribution and do a frequency count between intervals? To make inference about the population mean, we just directly calculate intervals from the posterior distribution. No where was the sampling distribution of the sample mean involved. Using MLE, we determine the posterior distribution of the population mean. Let's say we assume the prior distribution of population mean is uniform. Seems like in Bayesian Stats, we don't need the sampling distribution of the sample mean to make inferences about the population mean. Knowing that, we can test to see what is the % chance the population mean falls within some range, using the sampling distribution. We know the sampling distribution of the sample mean follows a normal distribution with mean = population mean and variance = population variance/ sample size. In Frequentist stats, we calculate the sample mean and sample variance from observed data.
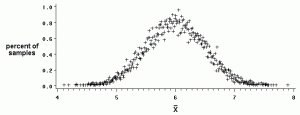
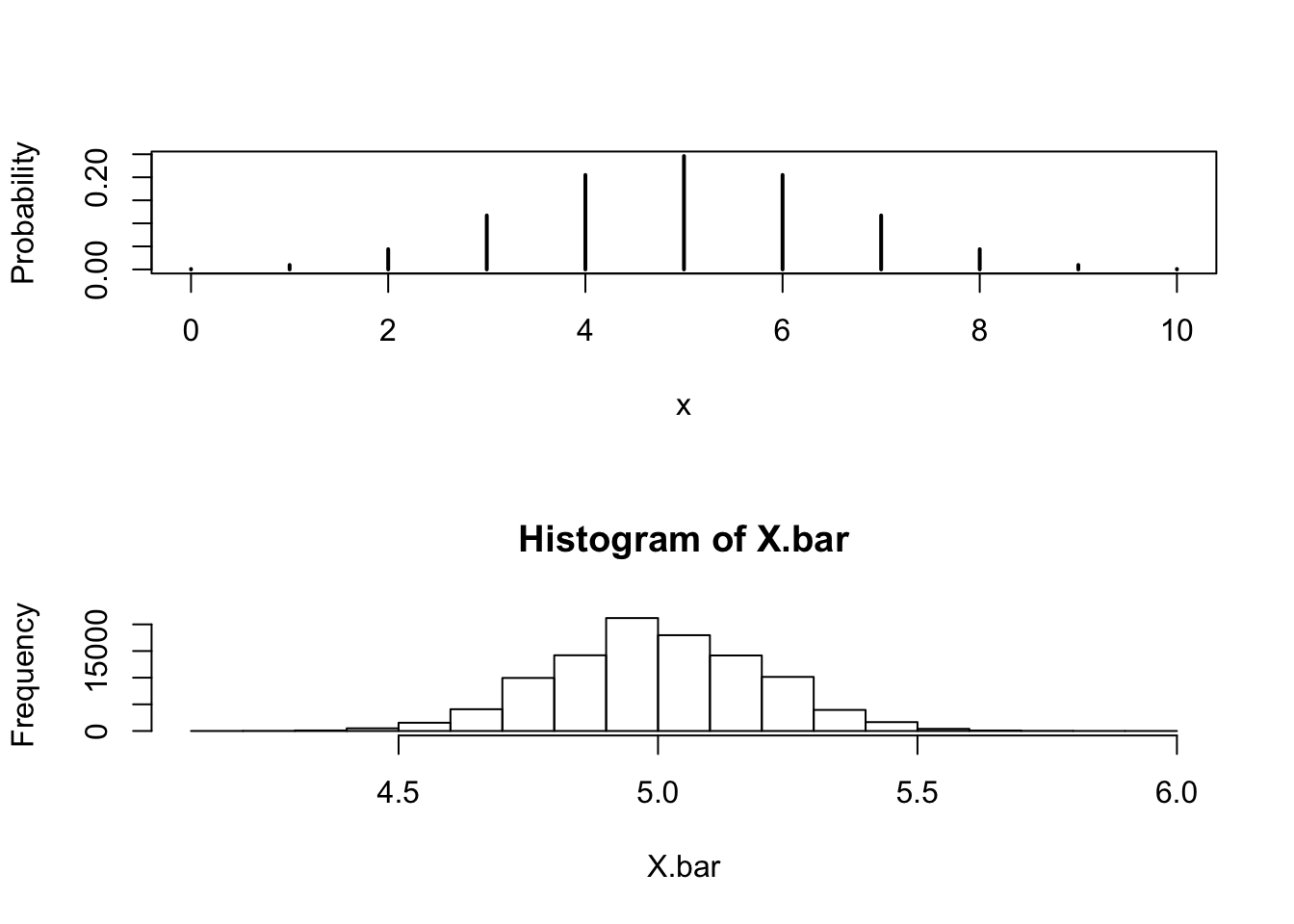
Let's take the classic case where the population follows a normal distribution, observations are iid, and we want to estimate the mean of the population.


 0 kommentar(er)
0 kommentar(er)
